Stochastic Reachability Toolbox

SReachTools focuses on the problem of stochastic reachability of a target tube1 — Construct controllers and characterize the set of initial states such that

  1. the controller satisfies the specified control bounds,
  2. the stochastic system stays within a time-varying target tube with a probability above a given threshold.

For example, a typical reach-avoid constraint is to stay within a safe set to stay within the time horizon and reach a target set at the time horizon when starting from an initial state \(\overline{x}_0\), as shown in the figure below.

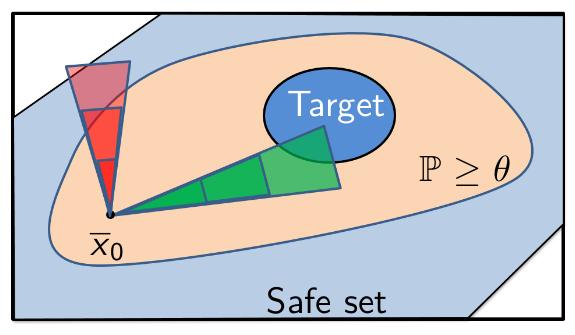
A cartoon depicting the stochastic reach-avoid problem

Here, we would like to pick the green controller over the red controller and compute the collection, the orange set, of all initial states such that the probability of success (reach-avoid) \(\mathbb{P}\) is above a given threshold \(\theta\).

This problem appears in a wide range of applications — space applications (spacecraft rendezvous and docking problem), transport (semi-autonomous/fully-autonomous cars and airplanes), biomedical applications (automated anesthesia delivery system), to name a few. Some of these examples have been analyzed using SReachTools. See the examples folder.

Our approaches rely on convex optimization, stochastic programming, Fourier transforms, and computational geometry to provide scalable, grid-free, and anytime algorithms for stochastic reachability analysis of linear systems. Specifically, SReachTools tackles the stochastic reachability of a target tube problem 1,2 for stochastic linear (time-varying or time-invariant) systems. SReachTools can construct polytopic (over- and under-) approximations and (open-loop and affine) controller synthesis for this problem. Our solution techniques include:

  1. chance-constrained approaches3,4,
  2. Fourier transforms5,
  3. particle control (and Voronoi partition-based undersampling) 3,6,
  4. Lagrangian (set-operations)7, and
  5. dynamic programming8,9.

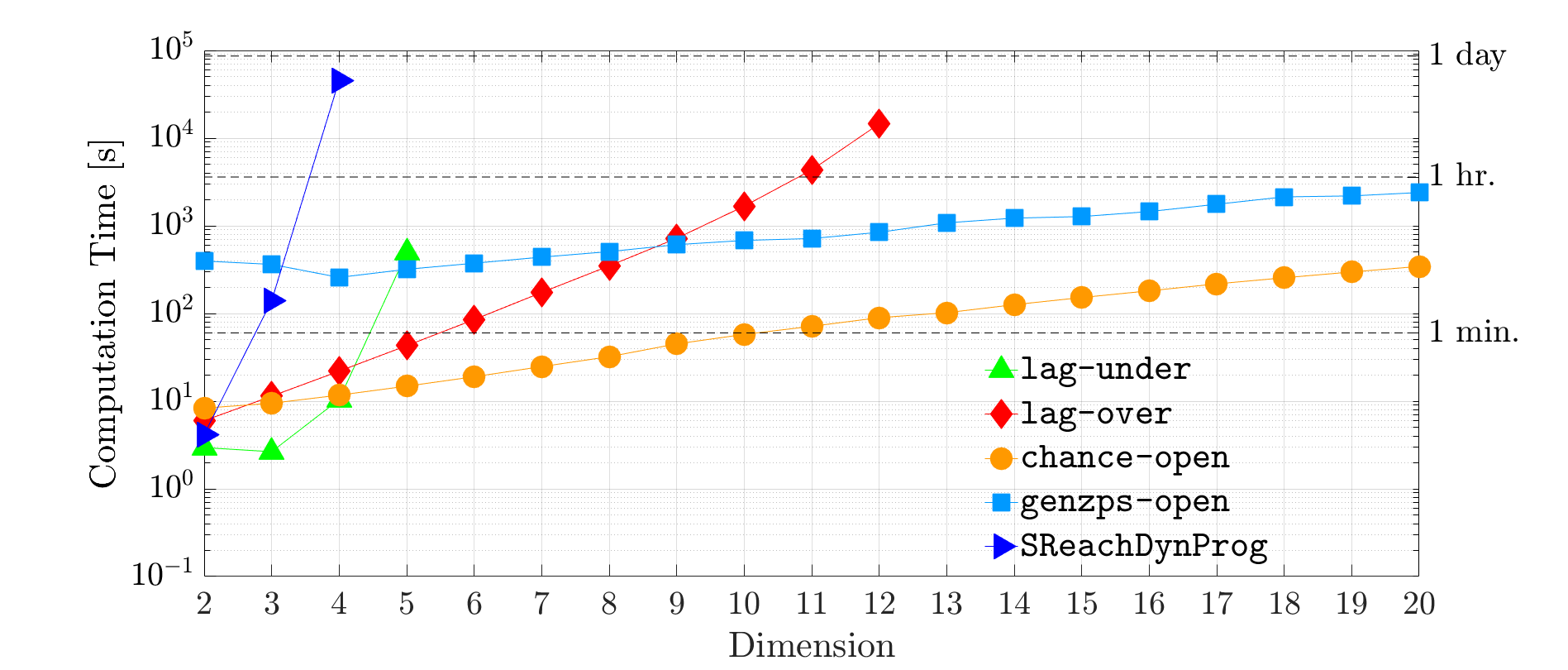
A cartoon depicting the stochastic reach-avoid problem

The above figure shows how SReachSet scales in the stochastic reach set computation for a chain of integrator dynamics, in comparison with the dynamic programming approach. Among these techniques, Lagrangian and particle control (along with Voronoi-based extensions) can handle arbitrary disturbances.

SReachTools also provides APIs to analyze the forward stochastic reachability problem10 using Genz’s algorithm 11.

  1. A. Vinod and M. Oishi, “Stochastic reachability of a target tube: Theory and computation”, submitted to IEEE Transactions of Automatic Control, 2018 (submitted). ↩ ↩2

  2. A. Vinod and M. Oishi, “Scalable Underapproximative Verification of Stochastic LTI Systems using Convexity and Compactness”, in Proceedings of Hybrid Systems: Computation and Control, pp. 1–10, 2018. ↩

  3. K. Lesser, M. Oishi, and R. S. Erwin, “Stochastic reachability for control of spacecraft relative motion,” in Proceedings of the IEEE Conference on Decision and Control, pp. 4705-4712, 2013. ↩ ↩2

  4. A. Vinod and M. Oishi, “Affine controller synthesis for stochastic reachability via difference of convex programming”, in Proceedings of Conference on Decision and Control, 2019 (submitted). ↩

  5. A. Vinod and M. Oishi, “Scalable Underapproximation for Stochastic Reach-Avoid Problem for High-Dimensional LTI Systems using Fourier Transforms”, in IEEE Control Systems Letters (CSS-L), pp. 316–321, 2017. ↩

  6. H. Sartipizadeh, A. Vinod, B. Acikmese, and M. Oishi, “Voronoi Partition-based Scenario Reduction for Fast Sampling-based Stochastic Reachability Computation of LTI Systems”, In Proceedings of American Control Conference, 2019 (accepted). ↩

  7. J. Gleason, A. Vinod, and M. Oishi, “Underapproximation of Reach-Avoid Sets for Discrete-Time Stochastic Systems via Lagrangian Methods,” in Proceedings of the IEEE Conference on Decision and Control, pp. 4283-4290, 2017. ↩

  8. A. Abate, M. Prandini, J. Lygeros, and S. Sastry, “Probabilistic reachability and safety for controlled discrete time stochastic hybrid systems,” Automatica, 2008. ↩

  9. S. Summers and J. Lygeros, “Verification of discrete time stochastic hybrid systems: A stochastic reach-avoid decision problem,” Automatica, 2010. ↩

  10. A. Vinod, B. HomChaudhuri, and M. Oishi, “Forward Stochastic Reachability Analysis for Uncontrolled Linear Systems using Fourier Transforms”, in Proceedings of the 20th International Conference on Hybrid Systems: Computation and Control (HSCC), pp. 35-44, 2017. ↩

  11. A. Genz, “Quadrature of a multivariate normal distribution over a region specified by linear inequalities: QSCMVNV”, 2014. ↩